Revolutionizing Secure Computation:
An Introduction to Math-Lock's Fully Homomorphic Encryption

Math-Lock company:
Sam Rososhek: Ph.D., Professor, cybersecurity expert, Chief scientist and Co-Founder at Math-Lock
Ilya Rososhek: CTO and Co-Founder at Math-Lock
Nikolay Savin: R&D Leader and Co-Founder at Math-Lock

Prologue

Welcome to the third article in our series on Homomorphic Encryption. If you haven't already, we recommend reading our previous articles to gain a foundational understanding of the topic which is essential due to general complexity of understanding about Homomorphic Encryption. Previously we explained in depth and using simple language about Homomorphic Encryption and its use-cases. In this article, we will introduce a new approach to Homomorphic Encryption, developed by our team. Our team is led by Sam Rososhek, a Ph.D., professor, and cybersecurity expert with over 50 years of experience in the field of mathematics, and over 35 years of experience in cryptography and cyber security. With numerous publications to his name, many you can find on ResearchGate, Sam is the inventor of all the fundamental research and algorithms behind our new approach. Assisting Sam is Ilya Rososhek, a lead developer of mathematical models, proof-of-concepts and prototypes in Python. And Nikolay Savin, our PostgreSQL, C, and web developer, who implemented our new scheme for Postgres. Our team has developed a new, practical, and highly efficient approach to Fully Homomorphic Encryption, and we're excited to share it with you. The article will be published on our website and posted on Linkedin. Let's dive in!

Introduction

Let's try to recall what we are here for: imagine that today you can encrypt all your data and send it to the cloud, encrypt your entire database and also send it to the cloud. But what's even more interesting is to continue working with this data as if it were standard plaintext, while performing all operations homomorphically without decrypting it ever. The key aspect here is, of course, the emphasis on data security, but no less important is the operational aspect. The speed of such encryption and working with encrypted data should be sufficient, which is absolutely impossible with existing schemes. However, we say that there is a scheme that allows working with data several orders of magnitude faster than any of the existing homomorphic schemes. In this article, we not only theorize but also demonstrate real-world practical solutions that have been implemented programmatically and are currently operational.

Technical introduction

Prior to describing our Homomorphic Encryption scheme, let us first distinguish the conceptual difference between our approach and all existing Fully Homomorphic Encryption (FHE) schemes. Broadly speaking, our team starts with developing fast and secure scheme and then further improves its security while building trade-offs between several layers of security and performance. In contrast, commonly used FHE schemes starts with "hardness assumptions'' (e.g., lattice problems, LWE, RLWE, etc.) to provide semantic security, and only then try to improve the speed through different optimizations that were not an inherent property in the original approach. When comparing these two approaches, the traditional bi-polar trade-off "security-performance" is extended to a triangle that includes "security-performance-usability." This means that in addition to the two main challenges of existing schemes - noise growth and computational complexity - we also address ciphertext expansion, which is the ratio of ciphertext bit length to plaintext bit length. This new factor is crucial for end-users. To illustrate, suppose company X wants to upload a database with a size of 2TB to the Cloud. Please note that 2TB is an abstract example which is very small for real life. If they use an existing FHE scheme, then according to theoretical approximations for the security parameter $$ \lambda $$ the best asymptotic estimation of ciphertext expansion is $$ O(\lambda^{2}) $$. It means that just for 128 bit length security ($$ \lambda $$ = 128 bit), bit size of ciphertext of 1 bit = $$ \lambda^{2}=(2^{7})^{2}=2^{14}=16384=2 $$KB. In this case almost pay-free 2TB of data will be converted after encryption to approximately $$ 10^{16} $$ bits, i.e. 10 petabit which already costs a lot of money, becomes very expensive to operate with, creates many limitations for adding more data etc This is a super optimistic approximation, and the actual ciphertext expansion is usually larger, as shown in the following article [3] and [Appendix A]. Additionally, the ciphertext bit length increases with homomorphic arithmetic operations, making the solution super expensive, not practical, and very slow. Could be that only cheating somebody can provide some operation performance for existing schemes but only by sacrificing security. See [Appendix A] for better understanding.
Therefore, one of the requirements of our HE scheme is that ciphertext expansion should not depend on the security parameter $$ \lambda $$. In other words, ciphertext expansion should be a constant value, preferably as small as possible. We would like to remind the reader that noise is used by all existing FHE schemes (with no exceptions) as a security factor to protect data, meaning that it’s exactly the security part of existing schemes.

General Part. Revolutionizing secure computation - getting into practical cryptosystems.

In our new approach we have fundamentally solved the problem of noise growth by not using it at all. And the security problems are solved by absolutely different ways and approaches. As for computational complexity, we changed the platform for computations and moved out from lattices to matrices of relatively small size which gives huge reduction of computational overhead.

The security basis of our approach.

Classical conjugacy search problem is to find $$ y\in G $$ in a way that for $$ m,x\in G, y^{-1}my=x $$ for noncommutative group G. Note, that here x is known but m and y are unknown. We use a more complex problem, namely, Hidden Conjugacy Search problem as follows: to find $$ y\in G $$ in a way that for $$ m,x\in G, y^{-1}my=\gamma x $$ for matrix noncommutative group G over scalar ring R with $$ \gamma \in R $$. Note that here only $$ \gamma x $$ is known but $$ ym, x $$ and $$ \gamma $$ are unknowns.
Furthemore, as first line of the defense access to ciphertext $$ \gamma x $$ for plaintext $$ m $$ has only a data owner with its private key. Only if an attacker can overcome this line of defense - he/she may try to solve Hidden Conjugacy Search problem. As the second line of defense, assuming that an attacker could get access to ciphertext and starts to solve Hidden Conjugacy Search problem - its solution $$ y $$ relates to “salted” plaintext $$ \gamma^{-1}m $$ but not to original plaintext $$ m $$. Our new computational platform offers several advantages over fixed rings of polynomials used in existing FHE schemes. Our scheme uses a ring of matrices, which allows for flexible conversion from one base ring to another. For instance it may be rings: $$ \mathbb{Z} $$ (integer numbers), $$ \mathbb{Z}_{n} $$ (residue rings on modulo n), ℚ (rational numbers), ℝ (real numbers), ℂ (complex numbers) and also rings of functions etc. It means that computations with matrices, for instance over ℝ shall be performed within the same arithmetic that in ℝ. In other words in floating-point arithmetic. Furthermore, our new platform uses relatively small matrices that drastically reduce computational overhead, resulting in a scheme that is many orders of magnitude faster than any existing scheme. For implementation we decided to choose two basic rings: $$ \mathbb{Z}_{n} $$ and ℝ, i.e. arithmetic of modulo residues on modulo n, using integer and/or floating-point arithmetic. The architecture of our HE cryptosystem looks as follows:

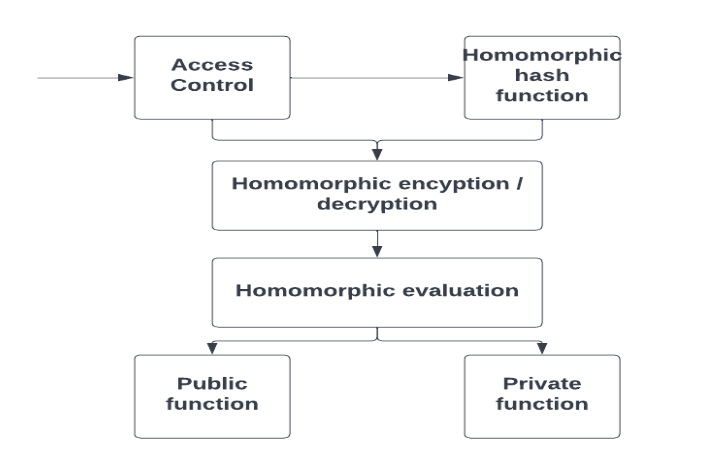
Thus our cryptosystem supports 3 main requirements to the security: confidentiality (encryption), authentication (access control), data integrity (Homomorphic hash function). Beside that, homomorphic evaluation gives privacy-preserving computations of public or private function over plaintexts.
Now let’s take a look at every separate block:

Access control.

It’s implemented in our system using a public key encryption scheme, which was previously developed in [1] and [2]. Access is granted through a specially designed authentication protocol, which requires users to demonstrate their knowledge of the private key. It is important to note that we have abandoned the definition of a pure public key and have instead introduced the concept of an "encryption key," which is not publicly accessible except by trusted users. This key serves as an owner's identifier that grants access to encrypted data. It should be noted that the key generator in this component of our cryptosystem is capable of generating additional key pairs (encryption key, decryption key) for privacy-preserving communication with other data owners.

Homomorphic hash function.

This is our proprietary function, which is better and stronger than typical SHA1, SHA2, SHA256 etc. This block provides data integrity using the function implemented as Homomorphic MAC protocol.

Homomorphic encryption / decryption.

This component is the most important and critical part of our cryptosystem. Our encryption scheme is unique when compared to all existing fully homomorphic encryption (FHE) schemes, as it is a "symmetric key" scheme. The transition from the authentication key-pair in the "Access control" block to the symmetric key is performed using our proprietary transformation, which is a critical component of our know-how. Symmetric key encryption provides fast encryption, which can only be performed by the owner of the symmetric key and the authentication key-pair. This configuration makes theoretical attacks with access to the encryption/decryption engine with adaptively chosen plaintexts or ciphertexts irrelevant. Even if an attacker attempts to generate ciphertext by themselves by generating a random matrix, it would be prevented by comparing the hash value of this matrix with the hash values of actual ciphertexts. Our encryption scheme provides robust security and privacy for all types of data.

Homomorphic evaluation.

Two basic homomorphic operations on ciphertexts-matrices, precisely Homomorphic Addition (HAdd) and Homomorphic Multiplication (HMult) can be performed via matrix addition or multiplication respectively. Resulting matrix-ciphertext contains the result of such operations, having elements of basic ring $$ \mathbb{Z}_{n} $$ or ℝ corresponding to which ring was chosen. Depth of corresponding arithmetic circuit for given function F could be very high for ℝ and arbitrary high for $$ \mathbb{Z}_{n} $$. All four arithmetic operations: addition, subtraction, division and multiplication could be performed for matrices-ciphertexts analogously to the same operations for matrix elements. For example, the sum or product of two matrices-ciphertexts after decryption gives the sum or product of two given elements of the basic ring (ℤ or ℝ). But how to divide matrix A at matrix B? The answer is simple: matrix A multiplied at inverse of matrix B if result of division (A / B) exists in base ring, then for corresponding matrices-ciphertexts exists matrix $$ A/B=A*B^{-1} $$. Thus, we can use our cryptosystem for privacy preserving computations with the usage of all 4 homomorphic arithmetic operations in modular arithmetic and in floating-point arithmetic as well.

Product related part.

Practical solution? Yes indeed, the first one and the only one existing in the World, which can be used easily by anyone. While any existing solution based on common schemes shall be fine-tuned in a very fancy and complex way, taking into account a lot of parameters - which can be done only by real experts in the field, our solution doesn’t require any tuning. As we stated many times before, in our previous articles, users can forget about bootstrapping, noise and many other mandatory attributes following by using PALISADE, SEAL etc libraries. It has many orders of magnitude faster performance [Appendix A] compared to any other scheme, at the same time being more than just a scheme, but the whole cryptosystem, which can be adopted to any organization and any need easily.

The fields of use are huge:

• Cloud computing - whatever which may go to the cloud and requires math. computations
• Databases - to work with them being fully encrypted and may be never decrypted
• Medical solutions (e.g. genomics computations, or various ML/DL algorithms)
• Automotive security - for securing communication channel and algorithms
• IoT - for securing devices and their communication
• Banking - for instance doing ML/DL computations to forecast potential revenue being fully encrypted
• And so on and so forth

Summary of what was implemented programmatically so far.

1. We have 2 fully functional python prototypes supporting integer and floating-point arithmetic which can be used easily by everyone with zero knowledge of how to configure or adjust the scheme. It just works out of the box with no use of noise, bootstrapping etc attributes of all other existing schemes (as stated many times before and in previous article N2 [4]
2. Both prototypes can do all 4 arithmetic operations including division - which is not possible in existing schemes at all.
3. Integer implementation has literally limitless multiplicative depth with zero ciphertext expansion, while any existing scheme has 20-50 operations and that’s it.
4. Floating-point implementation has limitations of approximately 200-250 operations multiplicative depth using about 13000 points precision accuracy with acceptable ciphertext expansion which correlates with simple multiplication of 2 numbers. If we divide or do subtraction - it doesn’t grow of course.
5. Several orders of magnitude faster performance compared to any existing homomorphic scheme.
6. PostgreSQL plugin which allows to store our data and perform homomorphic operations on ciphertext
7. Demo samples for a simple evaluations (with no respect to performance, due to REST API only way of use, since we not going to open our source code or algorithms)
8. Work in progress on cloud platform for secure computations using our FHE scheme.

API and Demo purpose.

We have an online Homomorphic calculator with UI for simple use.
Implemented REST API, whose demo samples can be found here - https://github.com/Math-Lock/fully-homomorphic-encryption-practical-and-fast and represented by 2 parts: 1) general sample to encrypt, decrypt data and perform arithmetic operations homomorphically. 2) db sample to work with PostgreSQL and our proprietary plugin for it. Sampe 1 shall be used to encrypt and decrypt data and sample 2 to post, query and perform homomorphic operations in PostgreSQL. Since this is only demo purpose solution consider to have all corresponding limitations, performance limitation (first of all due to REST and network connectivity) etc

Collaboration and potential customers.

We are ready to build/implement upon request a demo project to demonstrate what can be done by using our algorithms and solutions - FOR FREE. Also, we are working on a new platform to collaborate securely in the cloud doing computations on encrypted data without decrypting it ever (only once data downloaded from the cloud - somewhere in a far-far room, without light and under the carpet using private key)

Appendix A.
Explanation about performance. It’s a significant, complex and important addition to the article.

By intention it’s moved to the appendix, due to its very high complexity so here we are going to try to explain it with no formulas and just with basic explanation. Please make sure you read our article N2 [4] about existing schemes and libraries and some basic explanations what is FHE, its pros and cons etc.

Homomorphic encryption / decryption.

The performance of Fully Homomorphic Encryption (FHE) in the scope of existing schemes, such a PALISADE, SEAL etc can be understood by considering as minimum these several parameters:

• Latency: This refers to the time it takes for FHE operations to be performed. Lower latency means faster encryption and decryption of data.
• Noise growth: Noise is an unavoidable side-effect of FHE operations that can accumulate over time and affect the accuracy of the results. Lower noise growth means better accuracy and reliability of the encrypted data.
• Security: the level of security depends on the specific parameters used. In general, the larger the security parameters, the stronger the security, but the slower the FHE operations.
• Hardware requirements: FHE requires significant computational resources, including processing power, memory, and storage. The hardware requirements can affect the performance and scalability of FHE solutions.
• Library support: There are several FHE libraries available, and some libraries may perform better than others depending on the specific use case. The availability of documentation, community support, and updates can also be important considerations.

Overall, FHE performance is a trade-off between security, accuracy, speed, and hardware requirements. Security parameters are values that determine the level of security provided by an FHE scheme. These parameters are chosen based on the specific security requirements of the application and the available computational resources. Generally, the larger the security parameters, the more secure the FHE scheme, but the slower the performance. General amount of problematic configuration points varies within “asymmetry”, “serialization”, “negative computations'', “encryption parameters” and “ciphertext size”, “noise budget”, “recryption”, “bootstrapping”, “relinearization” etc. The two most common security parameters used in FHE schemes are the security level and the polynomial degree. The security level determines the probability of an attacker being able to break the encryption scheme. The higher the security level, the lower the probability of an attacker breaking the encryption. The security level is typically expressed in terms of the number of bits required to represent the security level. The polynomial degree determines the size of the coefficients used in the encryption scheme. The larger the polynomial degree, the more secure the scheme, but the slower the performance. The polynomial degree is typically expressed as a power of 2, such as 2048 or 4096. Other security parameters that may be used in FHE schemes include the ring dimension, the number of moduli used, and the error distribution used. These parameters can have an impact on the security and performance of the FHE scheme and are chosen based on the specific requirements of the application. It's important to note that choosing the appropriate security parameters for an FHE scheme requires a balance between security and performance. In general, a higher level of security requires larger parameter sizes, which can result in slower performance. Therefore, it's important to carefully choose the security parameters based on the specific needs of the application - having it in mind, we can definitely say that any existing company which is offering FHE so far - can suggest to potential customers very-very poor performance with high security. If they suggest acceptable performance or anything close (which is still slow) - it 100% means they are cheating with security and sacrifice it, generally speaking breaking the idea of secure computation on encrypted data.

FHE Performance additional complexity understanding (correlated only to existing schemes, it has nothing todo with our scheme).

In the context of FHE encryption, a performance metric is often measured in terms of the number of MVE (Million Ventil-Equivalents) processed per second. For example, a performance metric of 14.35 MVE/sec means that approximately 14.35 million units of digital circuit complexity were processed per second for FHE encryption. However, the amount of encrypted information per second depends on many factors, including the size of the encrypted data, the key length used, and other parameters. Therefore, it is not possible to accurately determine the number of bits of information that can be encrypted per second based on the MVE/sec metric alone. That’s why there are no articles which you can find with clear and simple definitions like how many bits per second scheme A gives compared to scheme B etc.
As stated in Table N2 in the article “New Insights into Fully Homomorphic Encryption Libraries via Standardized Benchmarks" [3], we can see how FHE performance (1 of aspects) look like and this is not standard understanding which a regular person can imagine like x amount of bits / second. No, it exactly demonstrates explained above theses about complex dependencies.
All in all to make it very short - authors of this article use 8-bit length word and 128 bit security key length. The most interesting thing for us here is floating-point operations. We can see that ciphertext size is up to 10 MBytes (raised from just 8 bits) while security params aren’t optimal and relatively small. Also, we can see that bars are indicating performance, where 1 bar is less than 100ms. We can see also, that there is no division here anywhere (all these libs as we explained before are not able to perform division). Furthermore - for multiplication every lib is awarded by 2 bars, which is marker for less than a second and this performance is just for 8 bits word to perform 1 single multiplication. Easy to imagine how slow FHE for all existing schemes is.

Math-Lock performance understanding.

As opposed to existing FHE schemes, Math-Lock doesn’t require any understanding about MVE/sec, any special tuning or configuration, any noise, bootstrapping, encryption parameters etc attributes. We operate always in the same way and manner for any security key length and any plaintext size. Performance can vary of course, but usage remains always the same. Below schemes demonstrate the following performance. Below you can see 3 images, used content and purpose described on every image.

- General performance

- Multiplicative depth

for 256/512 bit security and plaintext length, with precision 13K - 120K We done for floating-point and for integers 1024 bit security key with infinite multiplicative depth. Use-case with 10,000 multiplicative depth is just an example to indicate general performance

As we can see, at image N1 Math-Lock Python not optimized prototype gives 200,000 multiplications / sec or 2,000,000 additions for a plaintext of 256 bit and security key 512 bit, compared to PALISADE, SEAL etc 128 bit security key and just 1 multiplication per second with size of 8 bit plaintext.

Stay tuned! April, 2023

References

[1] S.K. Rososhek. New practical algebraic private key cryptosystem and some related algebraic and computational aspects. Applied Mathematics, v.4(7)., 2013, pp.1043-1049

[2] S.K. Rososhek. Modified Matrix Modular Cryptosystems. British Journ. in Math. and Computer Science, v.5, Issue 5 (2015), pp.613-636.

It should be noted that in article [2.a] that was published, where an analysis was conducted on our previously developed general cryptosystems (not FHE), as requested by us. The researchers identified some vulnerabilities which we were able to successfully and easily address already in 2019, thanks to their valuable insights. And generally speaking this article proofs our crypto-resistance, since they could not solve conjugacy search problem and random "salt" while attacking using linear decomposition method.

[2.a] Vitaliĭ Roman'kov. Cryptographic analysis of the Modified Matrix Modular Cryptosystem. https://arxiv.org/abs/1811.09876

[3] https://eprint.iacr.org/2022/425, “New Insights into Fully Homomorphic Encryption Libraries via Standardized Benchmarks”, page16, table II - noise growth and latency of core operations for integer, binary and floating-point encodings.

[4] Homomorphic encryption. Part2. “Existing schemes and programmatic implementations”